Assessing the performance of a large language model can be quite challenging. Traditional performance metrics like F1-score, precision, and recall are not directly applicable, posing a significant challenge for anyone working with them in production.
One major issue is the difficulty in effectively comparing different large language models (LLMs). Many companies we’ve engaged with resort to manual comparisons. They typically select a set of questions and rely on employees or a team to determine their preference for each model’s answers. While it’s a valid method, it remains an essentially qualitative experiment, heavily influenced by individual opinions.
Additionally, recent research indicates a decline in the performance of well-known OpenAI LLMs over time. You can read more about this in the study titled “Exploring the Impact of Temporal Dynamics on Language Model Evaluation.” This discovery underscores the increased significance of continuously assessing the performance of your chosen LLM.
So, how can we approach the evaluation of LLMs in a more objective manner? This blog article will delve into a methodology rooted in mathematical analysis rather than subjective viewpoints. First, we will delve into the specifics of the math behind it followed by a framework for testing LLMs over time.
To compare the performance of two LLMs, or one LLM over time, we are going to use a concept called cosine similarity. Cosine similarity is the cosine of the angle between the vectors; that is, it is the dot product of the vectors divided by the product of their lengths.
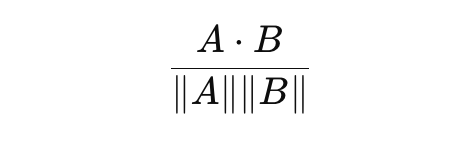
In simpler terms, cosine similarity helps us understand how similar two vectors are. Now, let’s see how this concept assists us in the assessment of LLMs. This is where embeddings come into play once more. If you’ve gone through our previous blog post on in-context learning, you’re familiar with the idea that we can represent any text as a vector by utilizing embeddings.
By doing so, we can compare two strings (pieces of text) by first using an embedding model to represent both as a vector and then compute the cosine similarity of those vectors.
Now that we know what cosine similarity is and how we can use it, we can look at a real-world example. Let’s compare the output of both GPT-3.5 and MPT-30B against a reference prompt and answer. We ask both models who is the president of the USA and what is his job. Or, more specifically:
Who is the united states president, and what is his job? Answer in no more than two sentences.
We can get a reference answer for this question by creating a two-sentence summary of the definition of the function of the US president by whitehous.gov.
The President of the United States serves as both the head of state and government, responsible for enforcing laws, leading the military, and conducting foreign diplomacy, with the current President being Joseph R. Biden. The President is elected every four years via the Electoral College, can issue executive orders, and has the power to sign or veto legislation, with a constitutional limit of two four-year terms — Reference answer.
The generated responses of the prompt are as follows for MPT-30B and GPT-3.5.
The president of the United States is the head of state and head of the federal government of the United States. Among the president’s many powers and responsibilities are the ability to make federal law with the help of Congress, to sign or veto legislation, to appoint federal judges and senior federal government officials, to convene and adjourn Congress on occasion, to grant pardons and reprieves to federal prisoners, to oversee the departments of the federal government and to command the U.S. military — MPT-30B answer
As of my last knowledge update in September 2021, the President of the United States is Joseph R. Biden Jr. His job is to serve as the head of state and government, responsible for executing and enforcing federal laws, directing foreign policy, and leading the executive branch of the U.S. government. Please verify this information as it might have changed since then. — GPT-3.5 response.
We can calculate the cosine similarity between our LLM response and the reference answer as follows:
Based on these numbers, we can conclude that both answers are close to the reference answer, but GPT-3.5 outperforms MPT-30B by a small margin.
We now have a quantitative comparison of MPT-30B and GPT-3.5. However, we should highlight there is one major drawback to this approach. It requires us to create a set of reference answers and questions which can be time-consuming and hard. But as we will see in the framework below, we only need to do this once and it enables a powerful measurement tool for LLMs over time.
By now, we know what cosine similarity is and how we can use it to test the performance of LLMs. Finally, let’s look at how we can apply these principles to monitor the performance of our LLMs over time.
To evaluate the performance of your LLM, we first need a ground source of truth and the associated prompts we are feeding our LLMs to generate a hopefully similar response. How many questions on which topics really depends on your use case, but we recommend you keep the following in mind.
Ensure your prompts are specific and limiting. For example, limit the maximum number of output sentences. If you are using in-context learning, ensure you always feed it the same information and limit the LLM’s response to only the data you feed it. Ensure your reference question mimics your real use case as close as possible. For example, there is no value in knowing that an LLM can correctly answer questions about the US president if your use case is answering questions about software engineering. This one seems obvious. But the important part here is that the reference questions need to reflect the work you expect the LLM to do for you. Once you have created your testing prompts and the reference answers, build a pipeline that checks these answers. How often you run this pipeline depends on your specific situation, we recommend you check it at least once a week and preferably every day. The sooner you catch any issues, the sooner you can address them.
An LLM performance measuring pipeline might look something like this.
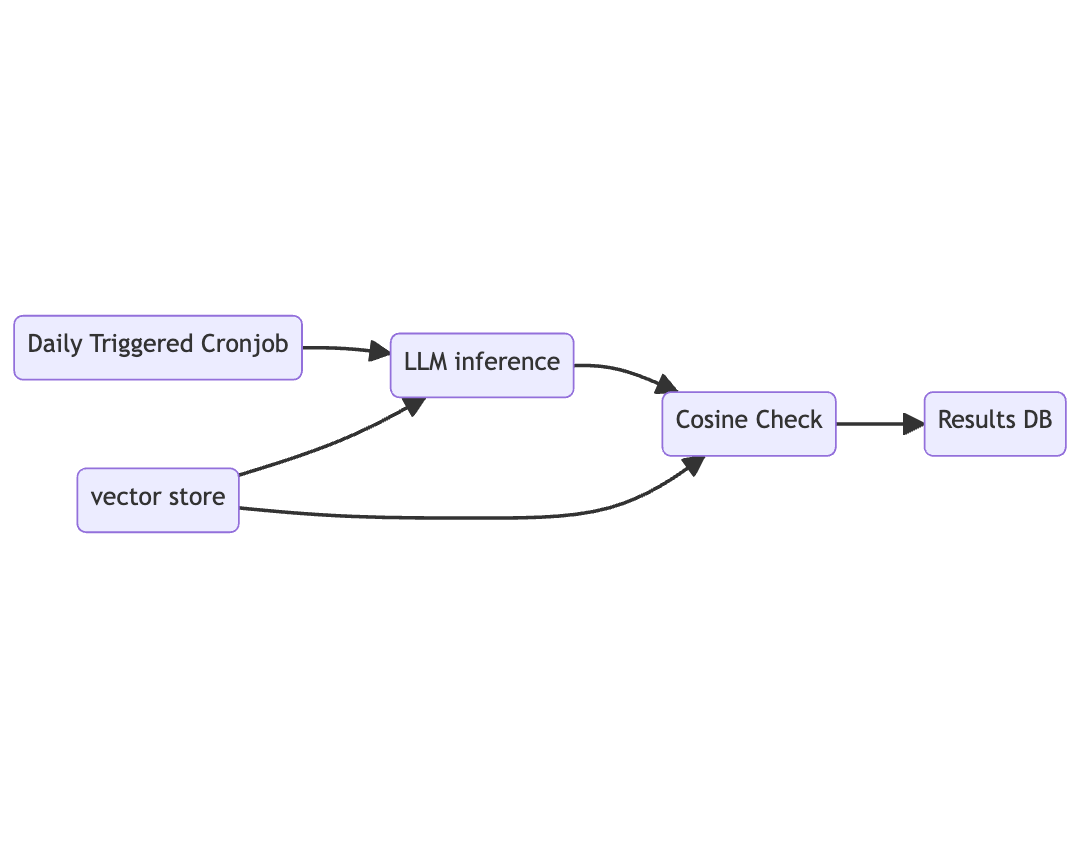
Our pipeline is triggered by a cronjob, on a daily basis and consists of three functions. We store our prompts, reference answers, and their embeddings in a CloudFlare Vectorize store which we add as a resource to the LLM inference function and the cosine check function. In the LLM inference check, we run each prompt through the LLM and pass the answer along to the cosine check function. In the cosine check function, we create vector embeddings of the new inference results and compare them to our reference embeddings stored in the Vectorize index. Results are stored in a SQL store at the end of the pipeline.
Over time you build up insights on the LLM performance in your specific domain. We can build out specific triggers to notify us over Slack, email, or any other tool if the performance of the LLM drops below a certain value; i.e., if my cosine similarity is less than .6, send a notification.
While this is an excellent approach to evaluating an LLM performance over time, we should not overlook the downsides.
In conclusion, the mathematical comparison of LLMs with each other or reference answers can be a powerful tool to use as a quantitative measure of correctness. It can help take the human out of the loop (once the reference questions and answers are drafted) and enable automated testing of LLM performance over time.